Por Manuel López Michelone
Desde que los científicos del cómputo decidieron tomar en sus manos el problema de hacer un programa que jugase bien al ajedrez, el enfoque más exitoso fue hacer una búsqueda para encontrar las jugadas correctas. Cualquier programa moderno hace un árbol de jugadas y respuestas, a profundidades de 4, 5 o más movimientos, y a través de una función de evaluación (que se calcula en los nodos terminales), se decide la mejor jugada. Sin embargo, ha habido una serie de intentos que se enfocan en que las máquinas jueguen como los mejores ajedrecistas sin tener que evaluar tantos nodos. De hecho, por ejemplo, Deep Blue, la máquina que le ganó un encuentro a Kasparov, podía calcular unas 200 millones de movimientos por segundo, mientras que el presumiblemente mejor jugador de todos los tiempos a lo mucho podía calcular 5 jugadas por segundo.
La pregunta es pues ¿qué hace un ser humano como Kasparov para hallar la mejor jugada sin tener que analizar millones de movimientos por segundo? Y esta cuestión la decidió atacar Erick Bernhardsson, tal vez sólo por diversión, pero los resultados de su investigación parecen ser asombrosos. Recientemente las redes neuronales profundas han tenido un avance extraordinario y sorprende a muchos por su capacidad de reconocer cosas. Esto abre la posibilidad de preguntarse qué tan buenas pueden ser estas redes para aprende cosas basadas en lógica y estrategia, como por ejemplo, el ajedrez.

Esencialmente una red neuronal se puede usar para aprender una función a partir de datos. Por ejemplo, si se tienen los datos de consumo de gasolina en el país, una red neuronal puede predecir (extrapolar) estos resultados para saber cuánta gasolina se usará en los próximos años al ritmo de cómo van las cosas. Así pues, la red neuronal hace una función que extrapola el resultado y a diferencia de una tabla de valores dados de una función, la red neuronal puede predecir valores de datos que aún no se tienen.
El problema es que muchas veces, casi siempre en general, se tienen datos insuficientes para entrenar a la red neuronal, pero en esta investigación de Bernhardsson, la solución fue descargar 100 millones de partidas de ajedrez del servidor FICS (Free Internet Chess Server). La red neuronal propuesta tiene 3 capas de profundidad con 2048 neuronas por capa. La capa de entrada consiste en un conjunto de 12 bloques de 64 entradas. Cada bloque de 64 bits toma una posición de las piezas posibles en el ajedrez (hay Rey, Dama, Alfil, Caballo, Torre y Peón, y los hay blancos y negros, de ahí los 12). Mediante estos tableros de bits (bitboards), la red empezó a trabajar sobre los 100 millones de partidas para así sacar las características importantes de las mismas.
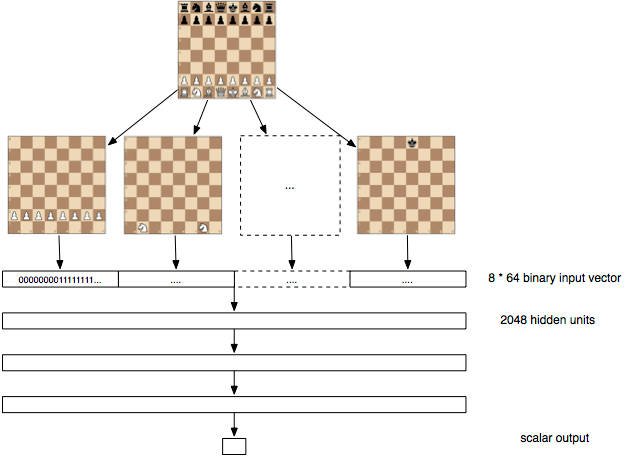
Bernhardsson decide entonces que la información de los datos (la partidas), es sobre una función de evaluación f(p) que le dice a uno la bondad de una jugada, donde p es 1 para un eventual triunfo, 0 para una eventual tablas (empate) y -1 para una eventual derrota. Se puede asumir que en un juego ideal, cada jugador hará las jugadas óptimas y entonces f(p) = -f(q) si la jugada q, hecha por el otro jugador, sigue q, y f(r) es mayor que f(q), donde r esa una jugada al azar. Estas reglas no son perfectas pero representan el comportamiento que uno querría tener de una función de evaluación.
La red neuronal fue entrenada presentando tripletas (p,q,r), por ejemplo la posición actual, la jugada seleccionada por el ser humano y la jugada al azar. La función objetivo, la que mide el error de la red, se diseñó para hacer que los pequeños errores correspondieran a las propiedades de la función de evaluación ideal.
Hay algunas cosas sorprendentes: Primero, no hubo un modelo de ajedrez, no se le dieron a la red las reglas del ajedrez ni se incorporaron al modelo. Segundo, la función objetivo es simplemente el permitirle a la red optimizar las propiedades teóricas de la función de evaluación y por ende, no hay sentido de “ganar” o “perder” interconstruido en el modelo. De hecho, éste no tiene idea del resultado final de cualquiera de las tripletas aplicadas. Esto significa que se está aprendiendo sin tener ninguna idea de quién gana es quien le está dando los datos. Los programas previos de ajedrez que usaban redes neuronales, por ejemplo el de Sebastian Thrun, NeuroChess, usaba el resultado final del juego para aprender a función de evaluación.
La pregunta sería: ¿Y este mecanismo aprende ajedrez? La respuesta asombrosa es que sí. La función de evaluación aprendida puede ponerse en cualquier motor existente de ajedrez y probarla contra la respuesta que un programa moderno funcionando vía fuerza bruta encuentra. El motor que usa esta función de evaluación se bautizó como Deep Pink, en honor a la máquina de IBM, Deep Blue. Se comparó contra Sunfish, un motor de ajedrez escrito en Python, el cual no es el mejor pero juega razonablemente bien.
La función de evaluación hallada por la red neuronal permite ganar 1/3 de las veces, lo cual no está mal como una primera aproximación. el científico dice que hay aún mucho trabajo por hacer. Y como veremos en la segunda parte de este artículo, veremos como en menos de un año cambiaron as cosas en esta idea de usar redes neuronales profundas para jugar bien al ajedrez.
Referencias:
Erik Bernhardsson
i-programmer
Fuente: unocero